本文来源于一道题目:以下递归函数存在栈溢出的风险,请问如何优化?
1 | function factorial (n) { |
普通递归
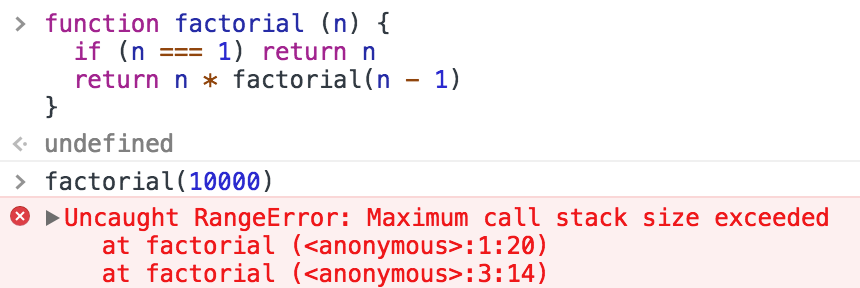
一看,递归没写退出条件,太 easy 了
1 | function factorial (n) { |
应该是题目故意埋的坑,当n很大的时候,仍会溢出,因为函数调用时会不断的压栈
文艺递归
出题者的意图应该是使用尾递归~~(见参考链接)
1 | function factorial (n, total = 1) { |
然而放在浏览器试下,factorial(10000)仍是溢出的。。
因为,ES6 的尾调用优化只在严格模式下开启,正常模式是无效的~
尾递归转化
1 | function tailCall (f) { |
当执行factorial(3)的时候,它会先在argsQueue.push([3, 1]),然后执行到while循环里,这时执行f.apply(null, [3, 1])其实才是真正要递归的函数。
然后又执行了factorial(2, 3),因此又在argsQueue.push([2, 3])。而由于前一次已经将active置位了,所以factorial(2, 3)就算执行结束了,无返回值
回到第一次的while里,发现argsQueue多了条[2, 3],于是继续调用f.apply(null, [2, 3])。同理,会执行factorial(1, 6),又在argsQueue.push([1, 6])。
再次回到第一次的while里,发现argsQueue又多了条[1, 6],于是继续调用f.apply(null, [1, 6])。而注意此时f(1, 6)直接返回total了,因此argsQueue里没有新增参数了,于是factorial就返回了value = 6
以上过程说白了仍是递归,区别在于普通递归时函数调用里继续函数调用,需要保存函数调用前的上下文(context)信息。而使用了尾递归转化后,递归调用时只会向共享的argsQueue里压入参数,在外层通过循环的方式(直到argsQueue为空)逐步调用函数主体。
总结
打个比方来说,普通递归的过程有点像深度优先遍历,函数调用一层层深入下去,需要不断保存 context 信息,最后再逐层回溯。因此函数调用栈是连续增长的,容易发生栈溢出。
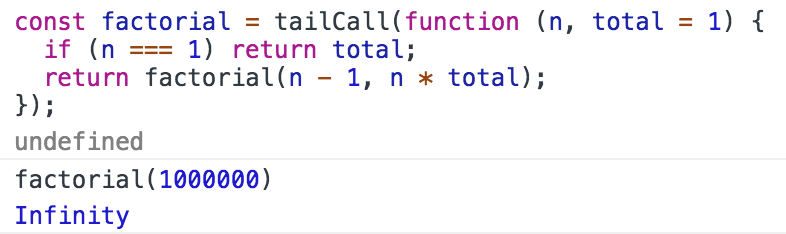
而尾递归优化后的递归过程就像广度优先遍历,函数调用后只在队列里增加一条参数,并不是逐层深入,而是通过循环逐渐执行函数体。因此函数调用栈是压入1次再弹出1次,不会发生溢出~
这是尾递归优化后的执行结果,虽然结果值已经超出 MAX_VALUE,但函数调用不会溢出
参考链接
stackoverflow: What is tail recursion?
ruanyifeng: 尾调用优化
ruanyifeng: es6尾递归优化